解方程是一个比较常见的功能,matlab,python都有简单方法实现。C++也有不少实现方法,下面就介绍一下GSL解方程的方法,代码参考了GSL源码中的demo。
GSL解方程的功能相对matlab要简单一些,目前看只支持实数解,并且只有一个解。当然对于大部分实际应用 已经足够了
假设需要解的方程组是如下2元非线性方程(方程右边不为0,移项一下就好了)
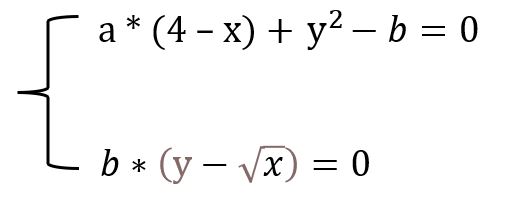
解方程的代码如下:
1.加入头文件
#include <stdlib.h>
#include <stdio.h>
#include <gsl/gsl_vector.h>
#include <gsl/gsl_multiroots.h>2.定义一个struct 保存可变常数
struct rparams
{
double a;
double b;
};3.定义方程
int rosenbrock_f(const gsl_vector * x, void *params,
gsl_vector * f)
{
double a = ((struct rparams *) params)->a; //常数a
double b = ((struct rparams *) params)->b; //常数b
const double x0 = gsl_vector_get(x, 0); //未知数x
const double x1 = gsl_vector_get(x, 1); //未知数y
const double y0 = a * (4 - x0) + x1*x1 - b; //方程1
const double y1 = b * (x1 - sqrt(x0)); //方程2
gsl_vector_set(f, 0, y0); //set 方程1
gsl_vector_set(f, 1, y1); //set 方程2
return GSL_SUCCESS;
}4.定义过程打印输出
int print_state_f(size_t iter, gsl_multiroot_fsolver * s)
{
printf("iter = %3u x = % .3f % .3f "
"f(x) = % .3e % .3e\n",
iter,
gsl_vector_get(s->x, 0),
gsl_vector_get(s->x, 1),
gsl_vector_get(s->f, 0),
gsl_vector_get(s->f, 1));
return 0;
}4.定义主函数
详细说明看注释
int main(void)
{
const gsl_multiroot_fsolver_type *T;
gsl_multiroot_fsolver *s;
int status;
size_t i, iter = 0;
const size_t n = 2; // n 定义了元的多少
struct rparams p = { 8.52550, 10.5665 }; // 定义常数a b 如果需要多次计算不同a b时的方程解,改这个p就可以了
gsl_multiroot_function f = { &rosenbrock_f,n, &p }; // 定义解方程的函数
double x_init[2] = { 10.0, 3.0 }; // 定义方程解预设值,这个值必须在真实解的附近,不然会解不出来。这个也是GSL的局限,我暂时没有找到解决的办法
gsl_vector *x = gsl_vector_alloc(n);
gsl_vector_set(x, 0, x_init[0]);
gsl_vector_set(x, 1, x_init[1]);
T = gsl_multiroot_fsolver_hybrids;
s = gsl_multiroot_fsolver_alloc(T, n);
gsl_multiroot_fsolver_set(s, &f, x);
print_state_f(iter, s);
do //这个循环迭代解方程,最多迭代1000次
{
iter++;
status = gsl_multiroot_fsolver_iterate(s);
print_state_f(iter, s);
if (status)
break;
status = gsl_multiroot_test_residual(s->f, 1e-7);//判断解是否是真实解
} while (status == GSL_CONTINUE && iter < 1000);
printf("status = %s\n", gsl_strerror(status));
gsl_multiroot_fsolver_free(s);
gsl_vector_free(x);
return 0;
}5.运行结果
可以看到运行7次后得到解。可以修改预设的解试试,当预设解偏离太多真实解时,就没办法得到解了。
iter = 0 x = 10.000 3.000 f(x) = -5.272e+01 -1.715e+00
iter = 1 x = 3.171 2.082 f(x) = 8.419e-01 3.189e+00
iter = 2 x = 3.039 1.750 f(x) = 6.935e-01 7.627e-02
iter = 3 x = 3.120 1.760 f(x) = 3.637e-02 -6.537e-02
iter = 4 x = 3.128 1.769 f(x) = -4.847e-03 4.300e-03
iter = 5 x = 3.127 1.768 f(x) = -6.137e-05 4.227e-05
iter = 6 x = 3.127 1.768 f(x) = -2.508e-07 2.030e-07
iter = 7 x = 3.127 1.768 f(x) = 7.090e-10 -5.579e-10
status = success6.使用导数,加快运算速度
可以手动定义方程组的偏导数,来加快计算过程。代码如下:
大部分内容一样的,多了一步计算偏导数的过程,详见注释
#include <stdlib.h>
#include <stdio.h>
#include <gsl/gsl_vector.h>
#include <gsl/gsl_multiroots.h>
struct rparams
{
double a;
double b;
};
int
rosenbrock_f(const gsl_vector * x, void *params,
gsl_vector * f)
{
double a = ((struct rparams *) params)->a;
double b = ((struct rparams *) params)->b;
const double x0 = gsl_vector_get(x, 0);
const double x1 = gsl_vector_get(x, 1);
const double y0 = a * (4 - x0) + x1*x1 - b;
const double y1 = b * (x1 - sqrt(x0));
gsl_vector_set(f, 0, y0);
gsl_vector_set(f, 1, y1);
return GSL_SUCCESS;
}
int rosenbrock_df(const gsl_vector * x, void *params,
gsl_matrix * J) //定义偏导数
{
const double a = ((struct rparams *) params)->a;
const double b = ((struct rparams *) params)->b;
const double x0 = gsl_vector_get(x, 0); //未知数x
const double x1 = gsl_vector_get(x, 1); //未知数y
const double df00 = -a; // 方程1 对x的偏导数
const double df01 = 2 * x1; // 方程1 对y的偏导数
const double df10 = - 0.5 * b / sqrt(x0); // 方程2对x的偏导数
const double df11 = b; //方程2 对y的偏导数
gsl_matrix_set(J, 0, 0, df00);
gsl_matrix_set(J, 0, 1, df01);
gsl_matrix_set(J, 1, 0, df10);
gsl_matrix_set(J, 1, 1, df11);
return GSL_SUCCESS;
}
int rosenbrock_fdf(const gsl_vector * x, void *params,
gsl_vector * f, gsl_matrix * J)
{
rosenbrock_f(x, params, f);
rosenbrock_df(x, params, J);
return GSL_SUCCESS;
}
int print_state_fdf(size_t iter, gsl_multiroot_fdfsolver * s)
{
printf("iter = %3u x = % .3f % .3f "
"f(x) = % .3e % .3e\n",
iter,
gsl_vector_get(s->x, 0),
gsl_vector_get(s->x, 1),
gsl_vector_get(s->f, 0),
gsl_vector_get(s->f, 1));
return 0;
}
int main(void)
{
const gsl_multiroot_fdfsolver_type *T;
gsl_multiroot_fdfsolver *s;
int status;
size_t i, iter = 0;
const size_t n = 2;
struct rparams p = { 8.52550, 10.5665 };
gsl_multiroot_function_fdf f = {&rosenbrock_f,&rosenbrock_df,&rosenbrock_fdf,n, &p };
double x_init[2] = { 10.0, 3.0 };
gsl_vector *x = gsl_vector_alloc(n);
gsl_vector_set(x, 0, x_init[0]);
gsl_vector_set(x, 1, x_init[1]);
T = gsl_multiroot_fdfsolver_gnewton;
s = gsl_multiroot_fdfsolver_alloc(T, n);
gsl_multiroot_fdfsolver_set(s, &f, x);
print_state_fdf(iter, s);
do
{
iter++;
status = gsl_multiroot_fdfsolver_iterate(s);
print_state_fdf(iter, s);
if (status)
break;
status = gsl_multiroot_test_residual(s->f, 1e-7);
} while (status == GSL_CONTINUE && iter < 1000);
printf("status = %s\n", gsl_strerror(status));
gsl_multiroot_fdfsolver_free(s);
gsl_vector_free(x);
return 0;
}输出:
可以看到收敛的更快了一点
iter = 0 x = 10.000 3.000 f(x) = -5.272e+01 -1.715e+00
iter = 1 x = 3.171 2.082 f(x) = 8.419e-01 3.189e+00
iter = 2 x = 3.114 1.765 f(x) = 1.009e-01 7.523e-04
iter = 3 x = 3.127 1.768 f(x) = 1.384e-05 4.293e-05
iter = 4 x = 3.127 1.768 f(x) = 1.667e-11 2.346e-15
status = success